分治算法是系统的开始学算法以来所接触到的第一个算法,其中响当当的例子就是 mergeSort (归并排序),名气大到几乎什么课程的示例代码都会带到一些。刚好把分治算法的课程上完,作业也刚好写完,觉得有点心得于是就来记录一下,当作是个笔记。
分治算法
分治算法就是用“分而治之”的原理,把一个复杂的问题分成两个或更多的相同或相似的子问题,直到最后子问题可以简单的直接求解,原问题的解即子问题的解的合并。
大概的流程可以分为三步:分解 -> 解决 -> 合并。
- 分解原问题为结构相同的子问题。
- 分解到某个容易求解的边界之后,进行递归求解。
- 将子问题的解合并成原问题的解。
分治法能解决的问题一般有如下特征:
- 该问题的规模缩小到一定的程度就可以容易地解决。
- 该问题可以分解为若干个规模较小的相同问题,即该问题具有最优子结构性质,利用该问题分解出的子问题的解可以合并为该问题的解。
- 该问题所分解出的各个子问题是相互独立的,即子问题之间不包含公共的子问题。
sourse: OI Wiki - 递归 & 分治
比如说分治算法的常用例子之一,mergeSort (归并排序) 就是如此实现的。
mergeSort (归并排序)
我们的目标是将 [38, 27, 43, 3, 9, 82, 10] 排序,可以先把列表分解成小问题,这就是 divide 的部分。当列表被分成无数个长度为 1 的 sub-array 后,每个 sub-array 都是最优解 (因为只有一个元素,必定有序);之后把列表两两合并,这边利用的是双指针来进行排序,对两个有序列表从左往右遍历,找到最小值添加到返回值直到完成遍历,因此每次排序消耗是 n1+n2,树深度为 logn,总体复杂度为 O(nlogn)。
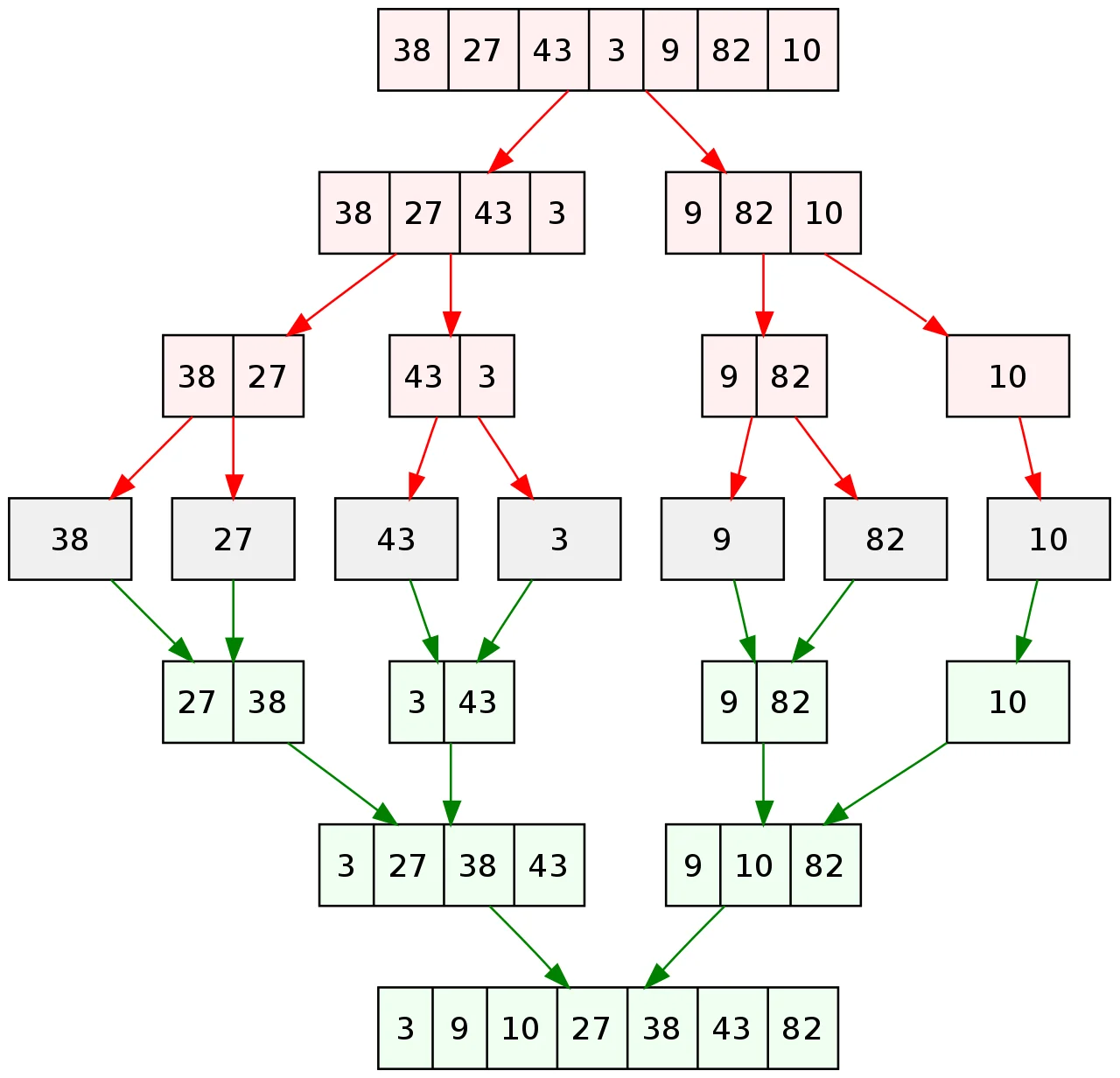
sourse: Wikipedia - Divide-and-conquer algorithm
# big o = l_n + r_n = 2n = n
def m_sort(l_arr, r_arr):
l_n, r_n = len(l_arr), len(r_arr)
i, j = 0, 0
ans = []
while i < l_n or j < r_n:
# run all elem from a list, attach other list
if i == l_n:
ans.extend(r_arr[j:])
j = r_n
elif j == r_n:
ans.extend(l_arr[i:])
i = l_n
# put min elem to ans
elif l_arr[i] <= r_arr[j]:
ans.append(l_arr[i])
i += 1
else:
ans.append(r_arr[j])
j += 1
return ans
# big o = nlongn
def merge_sort(arr):
n = len(arr)
if n < 2:
return arr
else:
l_arr = merge_sort(arr[:n//2])
r_arr = merge_sort(arr[n//2:])
return m_sort(l_arr, r_arr)
ans = merge_sort([38, 27, 43, 3, 9, 82, 10])
print(ans)
# [3, 9, 10, 27, 38, 43, 82]
最小最大值
找最小最大值是比较简单的分治问题。目标是找到子问题的最小最大值,先把列表分解成无数个长度为 1 的 sub-array 后,每个 sub-array 都是最优解;之后把列表两两合并,比较两个列表的最小、最大数字并且返回,每次比较开销为 1,总体复杂度为 O(n)。
# big o = n
def min_max(arr):
n = len(arr)
if n < 2:
return arr[0], arr[0]
else:
l_min, l_max = min_max(arr[:n//2])
r_min, r_max = min_max(arr[n//2:])
return min(l_min, r_min), max(l_max, r_max)
ans = min_max([38, 27, 43, 3, 9, 82, 10])
print(ans)
# (3, 82)
Arbitrage (套利)
套利问题比找最小最大值稍微难一点,不仅 max 要在 min 右边还需要计算获利最大(其实就是profit = r_max - l_min)。套利目标是找到低买点和高卖点,并且买点在卖点左边 (先买才能卖)。
# big o = n
def arbitrage(arr):
n = len(arr)
if n < 2:
return 0, arr[0], arr[0]
else:
l_profit, l_min, l_max = arbitrage(arr[:n//2])
r_profit, r_min, r_max = arbitrage(arr[n//2:])
return max(r_max-l_min, l_profit, r_profit), min(l_min, r_min), max(l_max, r_max)
ans = arbitrage([38, 27, 43, 3, 9, 82, 10])
print(ans)
# (79, 3, 82)
Reverse Pairs (逆序对)
逆序对:在数组中的两个数字,如果前面一个数字大于后面的数字,则这两个数字组成一个逆序对。输入一个数组,求出这个数组中的逆序对的总数。
例如:[5,3,1,2] 的逆序对为 (3,1), (3, 2), (5, 3), (5, 1), (5, 2) 总共 5 个逆序对。
逆序对具体计算方法类似 merge_sort,但是要加上 rp 计算逆序对数量。当合并两个列表时,一旦 r_arr[j] 值小于 l_arr[i],表示出现了逆序对,此时把 rp++ 即可。
# big o = n
def merge(l, r, rp):
ans = []
ln, rn = len(l), len(r)
i, j = 0, 0
while i < ln or j < rn:
if i >= len(l):
ans.extend(r[j:])
j = len(r)
elif j >= len(r):
ans.extend(l[i:])
i = len(l)
elif l[i] <= r[j]:
ans.append(l[i])
i += 1
else:
ans.append(r[j])
j += 1
rp += len(l) - i
return ans, rp
# big o = nlogn
def merge_sort(arr, rp):
n = len(arr)
if n < 2:
return arr, rp
else:
l, rp = merge_sort(arr[:n//2], rp)
r, rp = merge_sort(arr[n//2:], rp)
return merge(l, r, rp)
arr = [5,3,1,2]
rp = 0
arr, rp = merge_sort(arr, rp)
print(arr, rp)
# [1, 2, 3, 5] 5
Matrix Multiplication
矩阵乘法也可以使用分治算法。把矩阵分成 sub-matrix,分别计算各个区域的值,然后再合并成大矩阵。
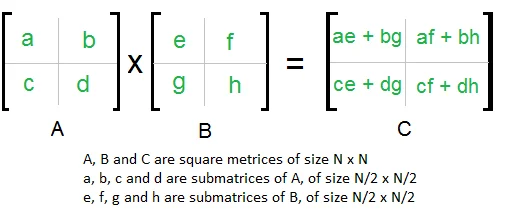
sourse: GeeksforGeeks - Divide and Conquer Set 5 (Strassen’s Matrix Multiplication)
总结
分治问题大概的流程可以分为三步:分解 -> 解决 -> 合并。
分治问题的模板包括:base case(n<1),分解列表(arr[:n//2], arr[n//2:]),递归和子问题答案的合并函数(magic)。
def magic(l_arr, r_arr):
pass
def divide_and_conquer(arr):
n = len(arr)
if n < 2:
return arr
else:
l_arr = divide_and_conquer(arr[:n//2])
r_arr = divide_and_conquer(arr[n//2:])
return magic(l_arr, r_arr)
不同的分治问题区别通常在于递归返回值(子问题答案)的数量,和合并最优解的函数,因此对于分治问题只要套用 merge_sort 模板再稍加改动就可以完成算法。
参考资料:

 美国攻略 ep5 日常用语套路总结
美国攻略 ep5 日常用语套路总结